Які теми з геометрії обов’язково потрібно знати? 7 клас.

Геометрія є одним із ключових розділів математики, що формує логічне мислення, просторову уяву та вміння розв’язувати практичні задачі. У 7 класі школярі знайомляться з базовими поняттями й властивостями, які є основою для подальшого навчання. Ретельне опрацювання цих тем є важливим не лише для старших класів, а й для успішного складання НМТ. У цій статті розгляньмо найважливіші теми з геометрії за 7 клас, які допоможуть краще зрозуміти основи та підготуватися до іспитів.

Які теми вивчаються в курсі геометрії 7 класу?

У 7 класі учні вивчають:

• Елементарні геометричні фігури та їхні властивості.

Вчимося усвідомлювати і пояснювати, що таке точка, пряма, «належати», «лежати між», розпізнавати та класифікувати геометричні фігури, співвідносити реальні об’єкти навколишнього середовища з моделями геометричних фігур, вимірювати і обчислювати довжину відрізків та градусну міру кутів.

• Взаємне розміщення прямих на площині.

Знайомимося з поняттями паралельності і перпендикулярності та обґрунтовано використовуємо їх при розв’язування завдань. Вводяться нові кути (суміжні, вертикальні, утворенні при перетині паралельних прямих січною), які важливі для подальших тем.

• Трикутники. Ознаки рівності трикутників.

У цій темі закладається база роботи з трикутниками. Працюємо з різними видами трикутників, їхніми елементами (бісектрисами, висотами, медіанами тощо), використовуємо властивості (рівнобедреного чи прямокутного) трикутників і ознаки рівності. Вчимося розуміти нерівності трикутників та співвідношення між сторонами і кутами трикутника. Можемо виділити властивість суми кутів трикутника: α + β + ɤ = 180°.

• Коло і круг.

Вчимося відрізняти коло від круга, коло, вписане в трикутник, чи описане навколо трикутника. Поглиблюємо знання новими видами кутів (центральними і вписаними). Розбираємо дотичну, яка точка є центром кола, вписаного в трикутник, і яка точка є центром кола, описаного навколо трикутника.

Що з програми 7 класу важливо знати на НМТ?

З курсу математики 7 класу маємо 1 важливу формулу, яка буде на НМТ: сума внутрішніх кутів трикутника дорівнює 180°. Записуємо її у вигляді формули: α + β + ɤ = 180°. 

Інших формул немає, проте значення, властивості, теореми та аксіоми використовуються в кожній задачі.

Приклади застосування матеріалу в завданнях НМТ.

Розгляньмо завдання, які були на НМТ з математики.

Приклад 1.

Розв’яжімо завдання розділу «Планіметрія». Тема: «Елементарні геометричні фігури на площині. Геометричні величини».

Три промені зі спільним початком лежать в одній площині (див. малюнок). Визначте градусну міру кута ɤ, якщо  α = 20°, β = 50°.

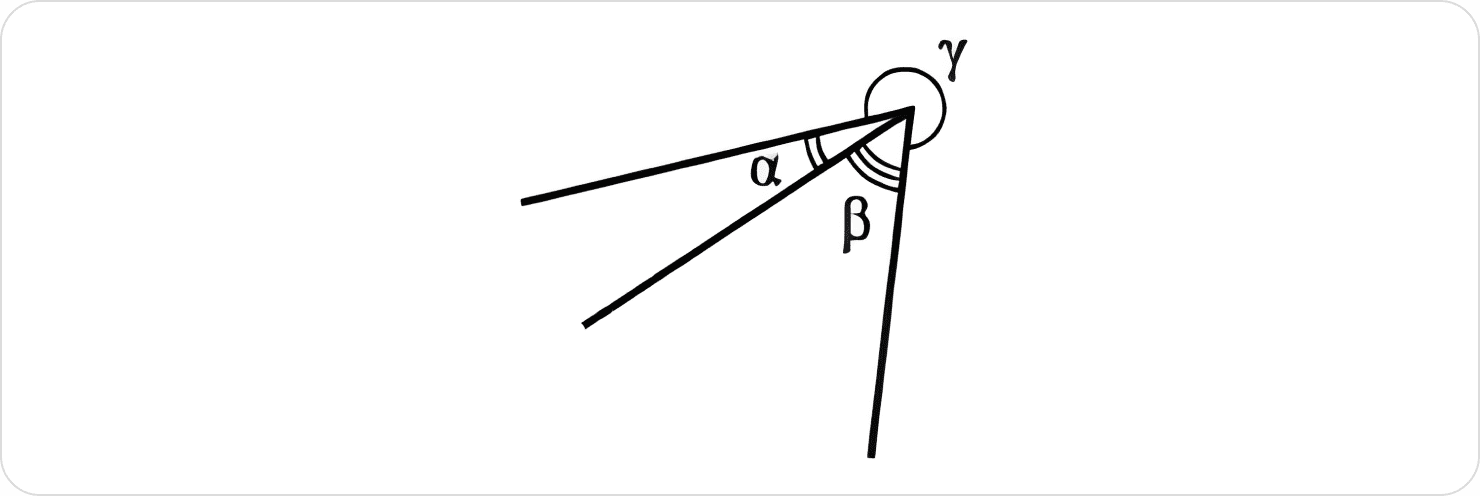
Це завдання перевіряє вміння вимірювати кути та знання аксіом планіметрії.

Градусна міра повного кута = 360°, тому α + β + ɤ = 360°.

ɤ = 360° - (a + ß)

ɤ = 360° - (20° + 50°)

ɤ = 290°

Відповідь: 290°.

Приклад 2.

Розв’яжімо завдання розділу «Планіметрія». Тема: «Елементарні геометричні фігури на площині. Геометричні величини».

Дві дороги розходяться на рівнинній місцевості як промені ОА і ОВ, позначені на малюнку. Перша дорога (промінь ОА) утворює кут 40° з напрямком «схід», а друга (промінь ОВ) – кут 20° з напрямком «південь». Який кут утворюють ці дороги між собою?

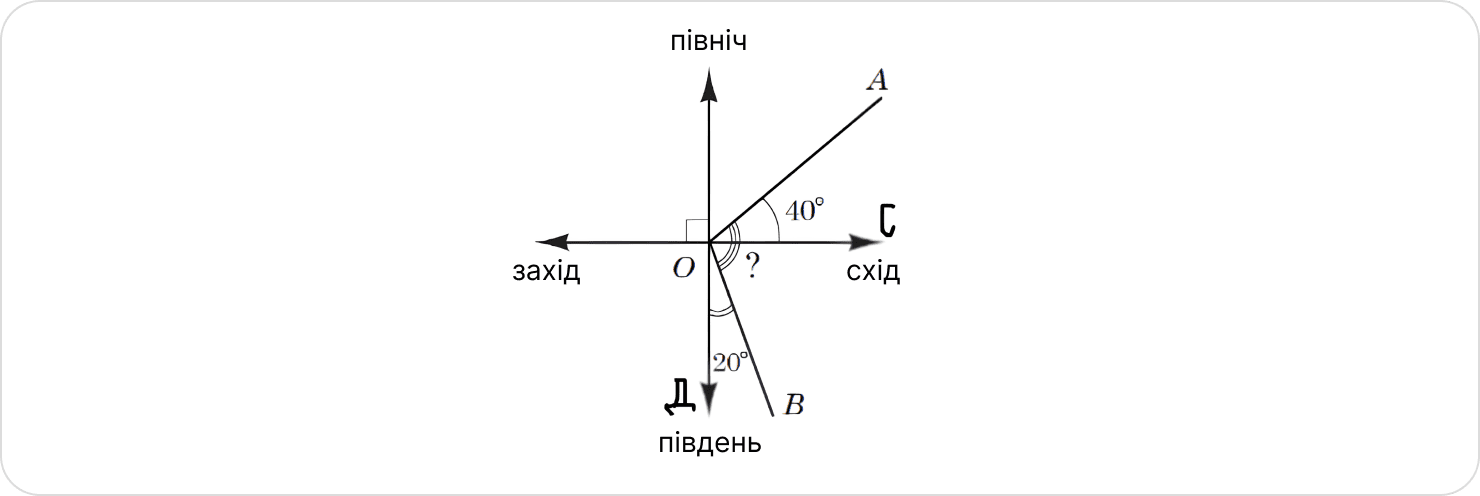
Це завдання перевіряє вміння застосовувати означення, ознаки та властивості найпростіших геометричних фігур до розв’язування задач практичного змісту.

Кут СОД = 90° (властивості прямого кута).

Кут СОВ — це різниця кутів СОД і ВОД, тобто 90° - 20° = 70°.

А кут АОВ — це сума кутів АОС і СОВ, значить, 40° +70° = 110°.

Відповідь: 110°.

Приклад 3. 

Розв’яжімо завдання розділу «Планіметрія». Тема: «Коло та круг. Многокутники».

Два кола з центрами в точках О і О1 мають внутрішній дотик (див. малюнок). Обчисліть відстань ОО1, якщо радіуси кіл дорівнюють 12 см і 8 см.

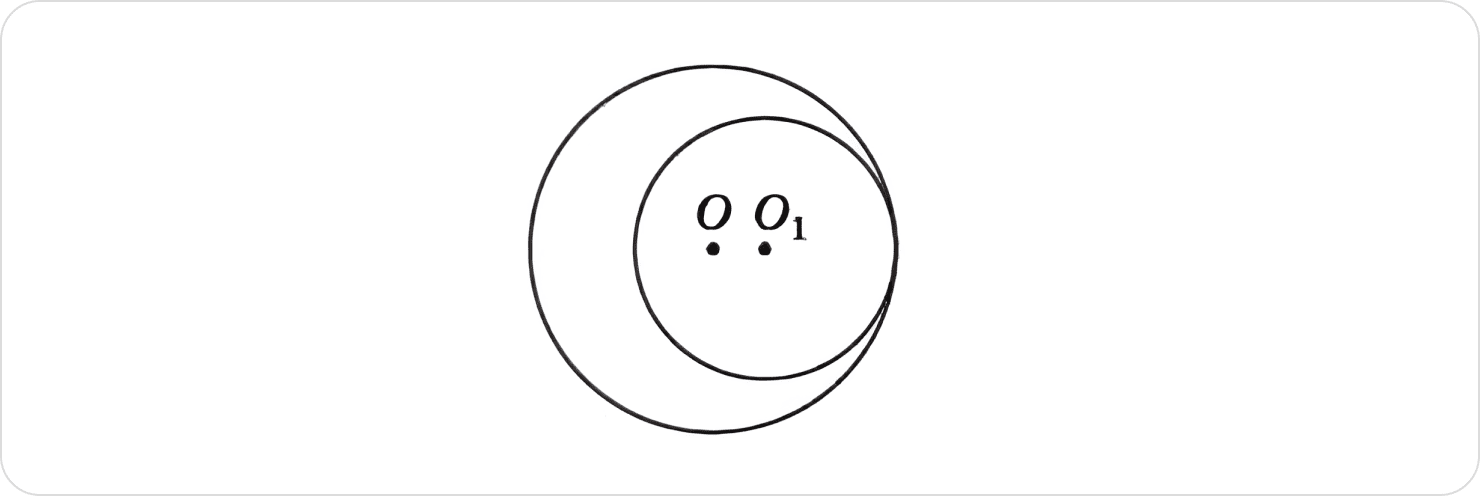
Це завдання перевіряє знання властивостей круга, його частин і розуміння довжини відрізків.

Зробимо додаткові побудови: позначимо точку дотику А, з’єднаємо центри кіл з А.

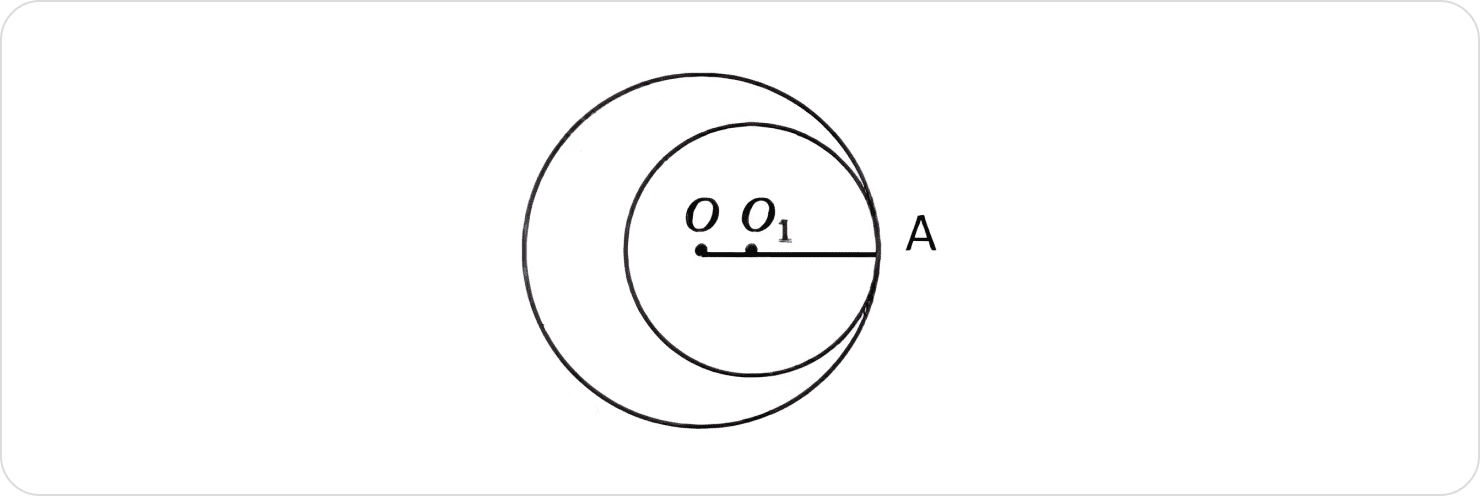
За умовою ОА = 12 см, О1А = 8 см.

Довжина ОО1 = ОА - О1А = 12 - 8 = 4 (см).

Відповідь: 4 (см).

Сподіваємося, що цей конспект стане вам у пригоді!

А якщо вам складно розібратися в даних темах самостійно — наші викладачі з радістю вам в цьому допоможуть!