Які формули з алгебри обов’язково потрібно знати? 7 клас.

Алгебра — це основа багатьох математичних процесів, з якими ми стикаємося щодня. У 7 класі учні знайомляться з ключовими формулами, які стають фундаментом для розв'язання складніших завдань у старших класах. Ці формули не лише допомагають зрозуміти алгебру, але й є обов'язковими для успішного складання НМТ. Ми підготували для вас невеликий конспект з найважливішими алгебраїчними формулами, які кожен семикласник повинен засвоїти для досягнення високих результатів на іспитах та для подальшого вивчення математики. А також підготували приклади розв'язання відповідних завдань.

Які теми вивчаються в курсі алгебри 7 класу?

У 7 класі учні вивчають:

• Лінійні рівняння з однією змінною

Вчимося розпізнавати лінійне рівняння з однією змінною; використовувати основні властивості рівняння; робити рівносильні перетворення; характеризувати випадки, коли лінійне рівняння з однією змінною має один розв’язок, має безліч розв’язків або не має розв’язків; створювати математичну модель задачі у вигляді рівняння; розв’язувати сюжетні задачі з реальними даними щодо: безпеки руху, розрахунку сімейного бюджету, можливості здійснення масштабних покупок, безпеки і охорони здоров’я та інших практичних аспектів фінансових питань.

• Цілі вирази

Вчимося працювати з числовими виразами та виразами зі змінними; приводити і записувати одночлени і многочлени до стандартного вигляду, зводити подібні члени; застосовувати формули для перетворення многочленів; розуміти сутність дії піднесення до степеня і використовувати властивості степеня з натуральним показником; додавати-віднімати, множити многочлени, розкладати многочлени на множники різними способами. Звертаємо увагу на формули скороченого множення та обчислення значень виразів.

• Функції

Вводиться сутність поняття функції і те, що пряма пропорційність є окремим видом лінійної функції; закладаються поняття аргументу, функції, області визначення функції, області значень функції, графіка функції. Вчимося знаходити за графіком функції значення функції за даним значенням аргументу і навпаки; визначати окремі характеристики функції за її графіком (нулі, додатні значення, від’ємні значення).

• Системи лінійних рівнянь з двома змінними

Вчимося застосовувати набуті раніше знання для побудови графіків лінійних рівнянь з двома змінними, використовуючи графічну інтерпретацію — випадки, коли система двох лінійних рівнянь з двома змінними має один розв’язок, має безліч розв’язків або не має розв’язків; визначати способи розв’язування системи двох лінійних рівнянь з двома змінними; створювати математичну модель задачі у вигляді системи рівнянь.

Які формули за 7 клас потрібно знати на НМТ?

Найважливіші формули:

1. Властивості степеня з натуральним показником:

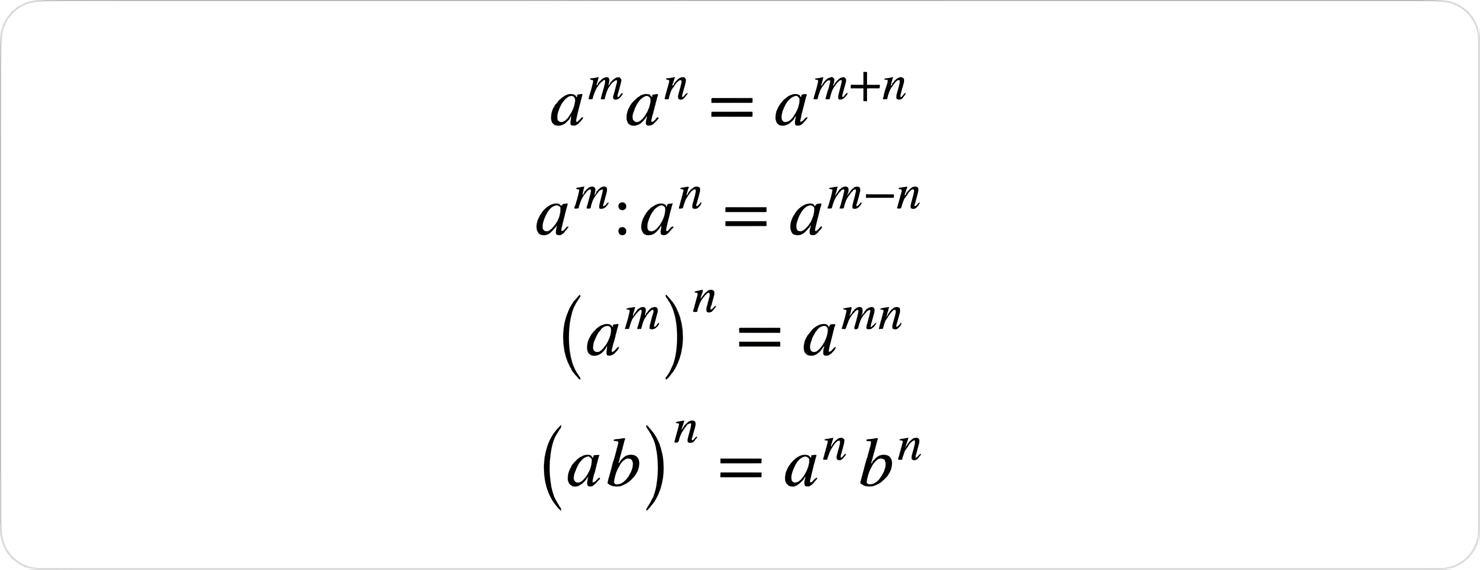
2. Формули скороченого множення:

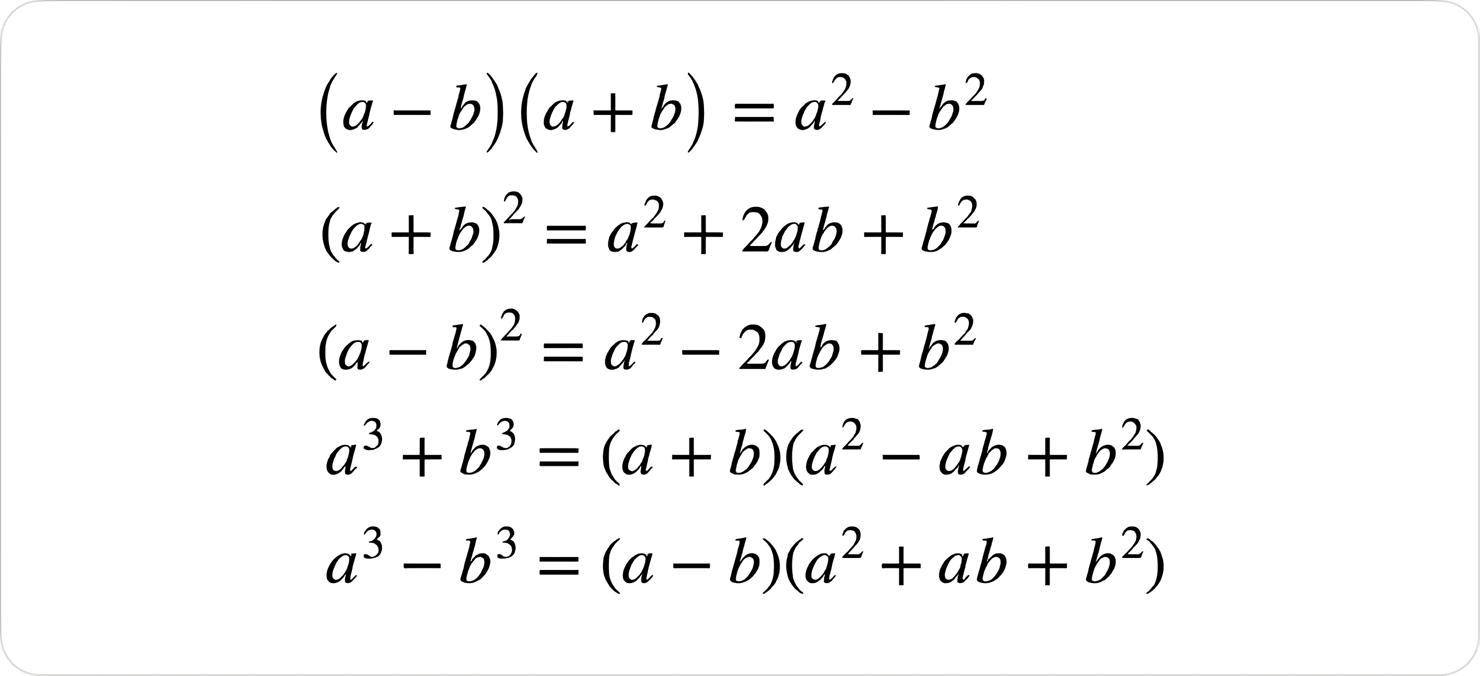
3. Лінійне рівняння з однією змінною:

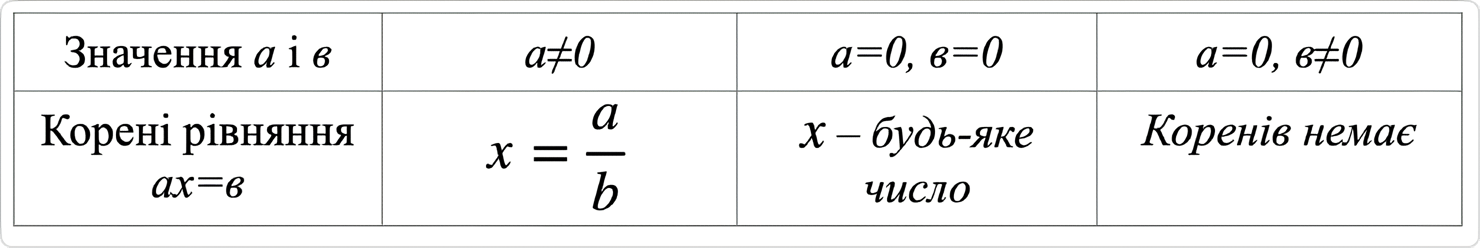
4. Функції:

Лінійна функція: y = kx + b, де k і b — деякі числа, x — незалежна змінна. y = kx, де k ≠ 0 — пряма пропорційність.

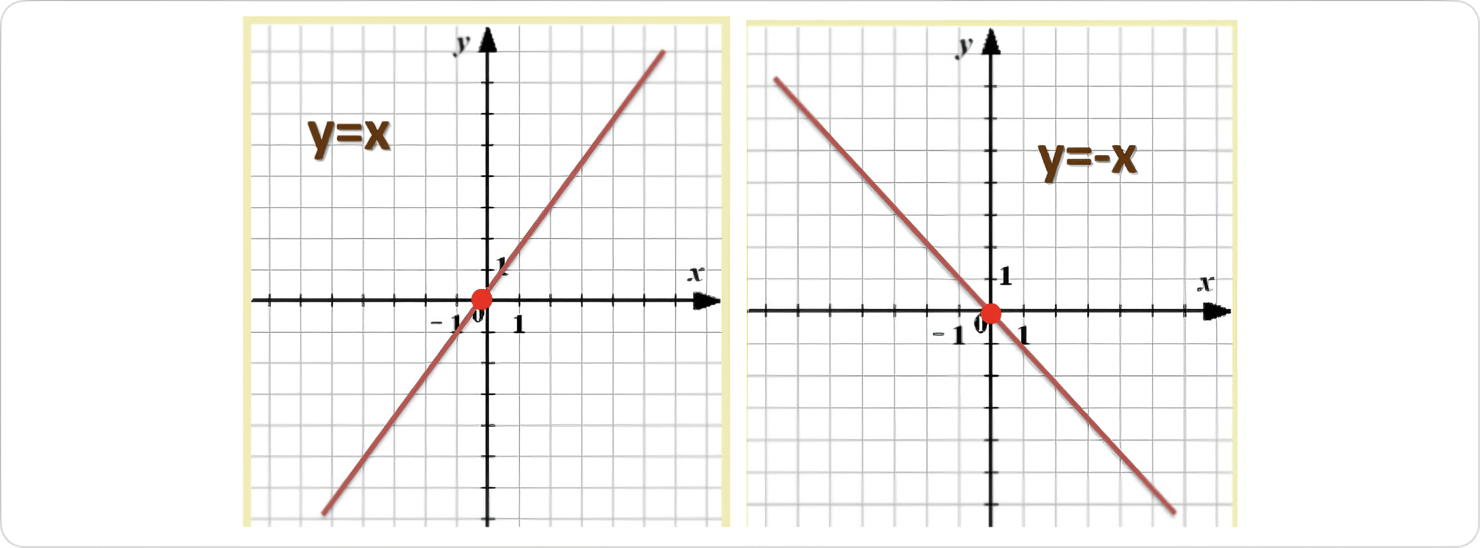
• Методи розв’язування систем двох лінійних рівнянь із двома змінними:

1. Графічний метод

2. Метод підстановки

3. Метод додавання

• Модуль

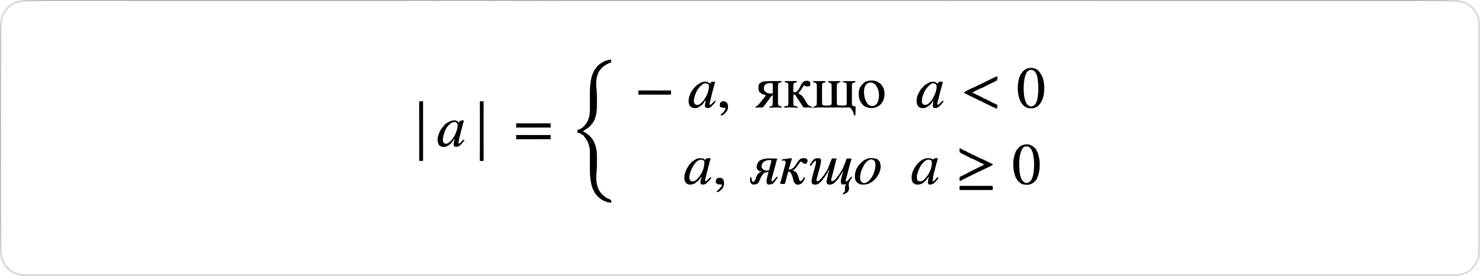
Приклади застосування формул в завданнях НМТ

Приклад 1.

Розв’яжімо завдання розділу «Рівняння, нерівності та їхні системи». Тема: «Лінійні, квадратні, раціональні рівняння та системи рівнянь».

Розв'яжіть рівняння

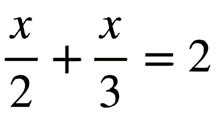
Це завдання перевіряє вміння розв’язувати лінійні рівняння й використовувати властивості.

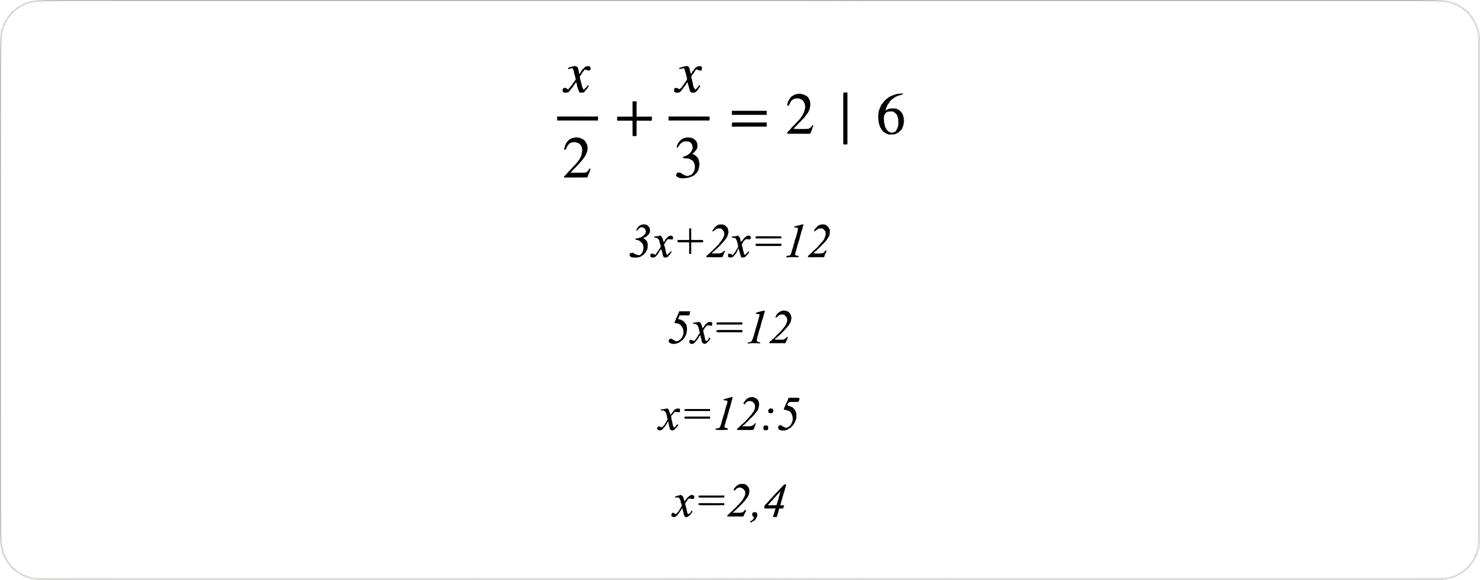
Приклад 2.

Розв’яжімо завдання розділу «Рівняння, нерівності та їхні системи». Тема: «Лінійні, квадратні, раціональні рівняння та системи рівнянь».

Розв’яжіть систему рівнянь

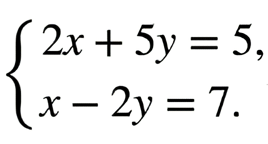
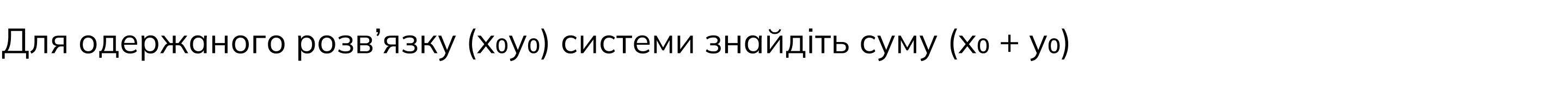
Це завдання перевіряє вміння розв’язувати лінійні рівняння та їхні системи.

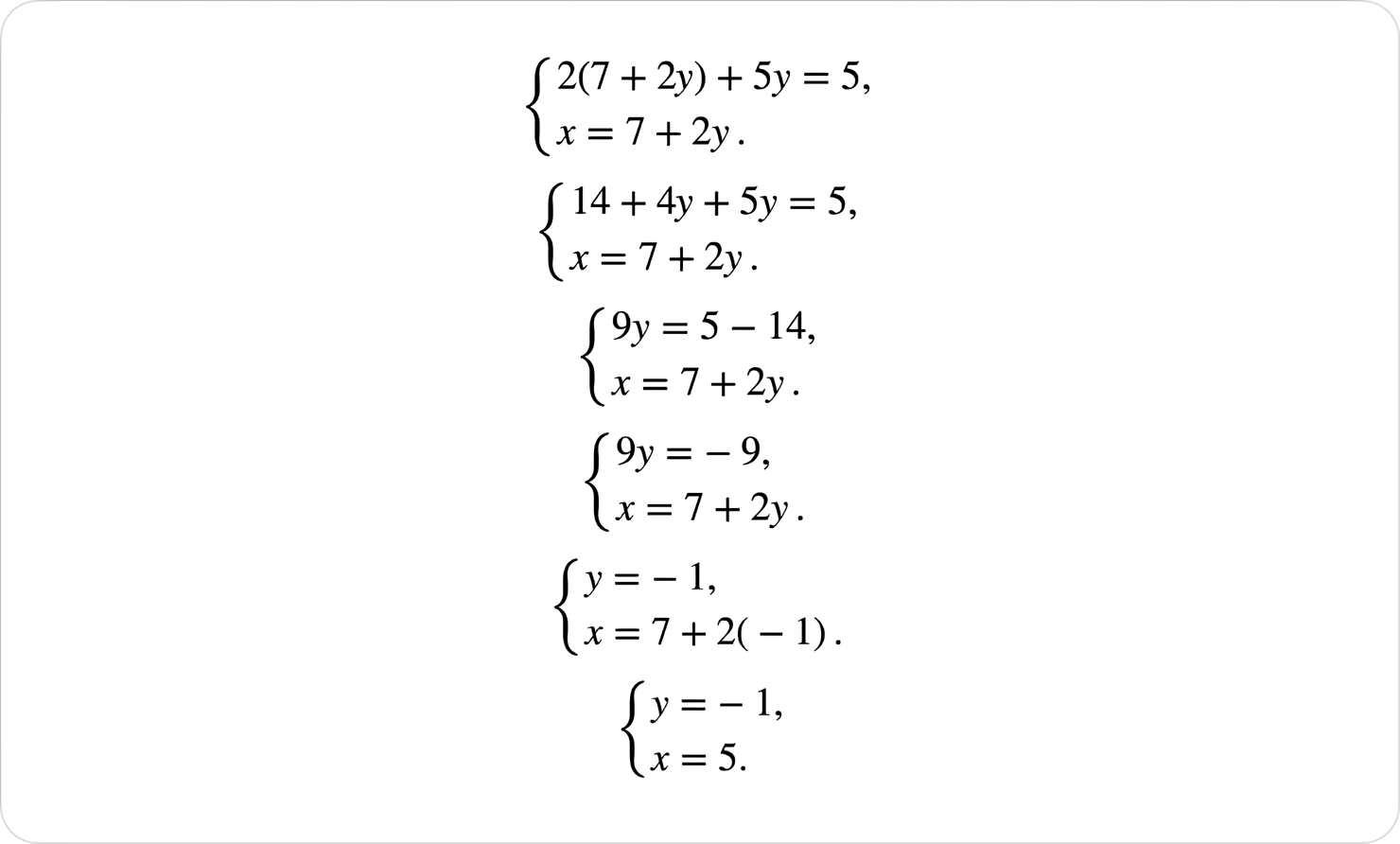
Отримали зв’язок (5; -1) і суму 5 + (-1) = 4.

Приклад 3.

Розв’яжімо завдання розділу «Рівняння, нерівності та їхні системи». Тема: «Лінійні, квадратні, раціональні рівняння та системи рівнянь».

Якщо рівняння має єдиний корінь, запишіть його у відповіді. Якщо рівняння має кілька коренів, то у відповіді запишіть їхню суму.

Це завдання перевіряє вміння розв’язувати рівняння, використовуючи властивості модуля та означення.

Якщо х ≥ 0, то |x| = x. Значить, х + 4х = 3, 5х = 3, х = 0,6.

Якщо х < 0, то |x| = -x. Значить, х - 4х = 3, -3х = 3, х = -1.

Відповідь: це сума 0,6 + (-1) = -0,4.

Сподіваємося, що цей конспект стане вам у пригоді!

А якщо вам складно розібратися в даних темах самостійно — наші викладачі з радістю вам в цьому допоможуть!