Що таке раціональні числа?

Математика — це мова логіки, точності й порядку. Але водночас вона надзвичайно цікава, особливо коли ми розуміємо, як саме влаштовані її поняття. Одне з таких понять — раціональні числа, які знайомі кожному ще з початкової школи, але набагато глибші, ніж може здатися на перший погляд. Ці числа постійно трапляються в обчисленнях, задачах, прикладних науках і фінансах.

Спробуймо разом зануритися в цю тему! Розгляньмо, що таке раціональні числа, якими бувають приклади, як їх записують і як правильно їх множити.

Які числа є раціональними? 

Раціональні числа — це числа, які можна представити у вигляді дробу:

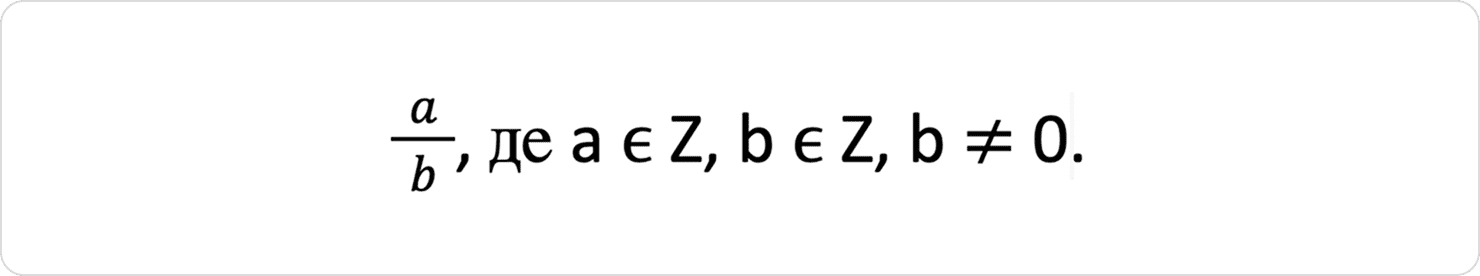
Тобто, раціональні числа — це відношення двох чисел, які можна подати у вигляді дробу, де чисельник і знаменник — цілі числа, а знаменник не дорівнює нулю (бо на нуль ділити не можна).

Раціональні числа можуть бути як додатними, так і від’ємними, а також дорівнювати нулю.

Цікаво, що слово «раціональний» походить від латинського «rationalis», що означає «розумний», «логічний», «пропорційний». І справді, раціональні числа — це впорядковані співвідношення, які дозволяють нам вимірювати, ділити й порівнювати.

Приклади раціональних чисел

Раціональні числа оточують нас всюди. Ось декілька прикладів, які показують, наскільки вони різноманітні:

1. Звичайні дроби

Прості дроби — класичні приклади раціональних чисел.

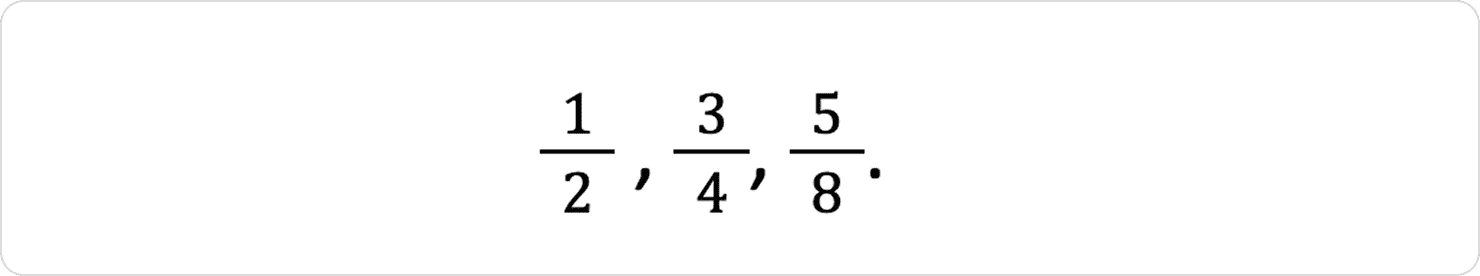
2. Цілі числа

Цілі числа — теж раціональні, бо їх можна записати у вигляді дробів.

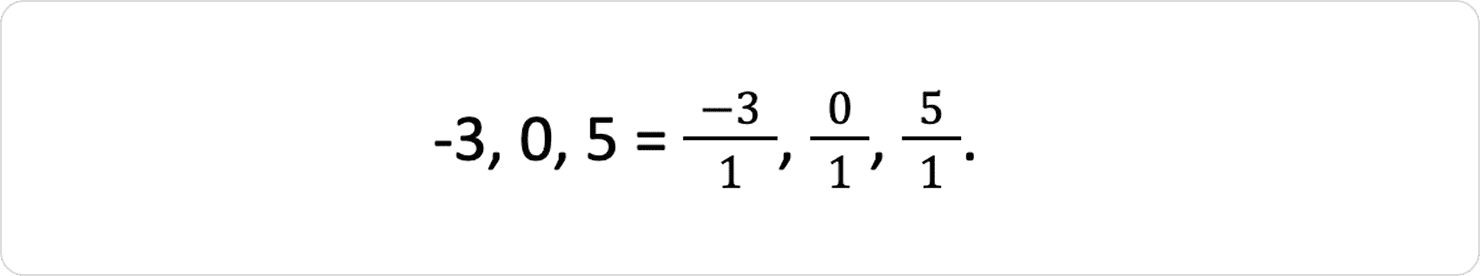
3. Десяткові дроби, що закінчуються

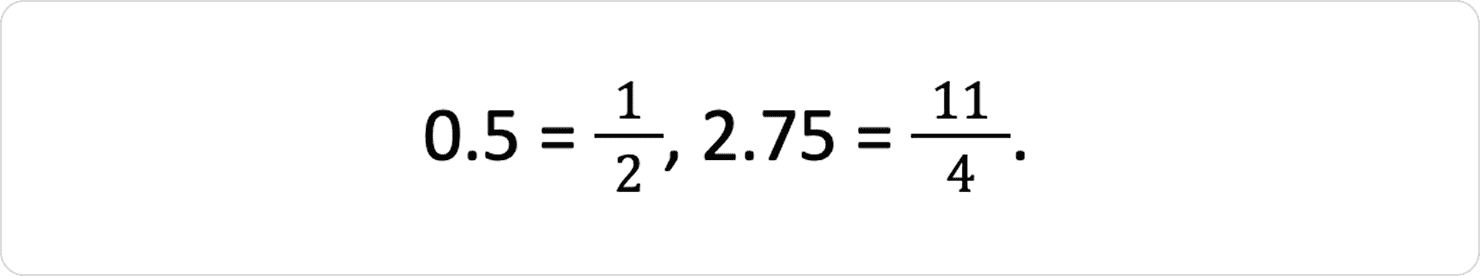
4. Періодичні десяткові дроби

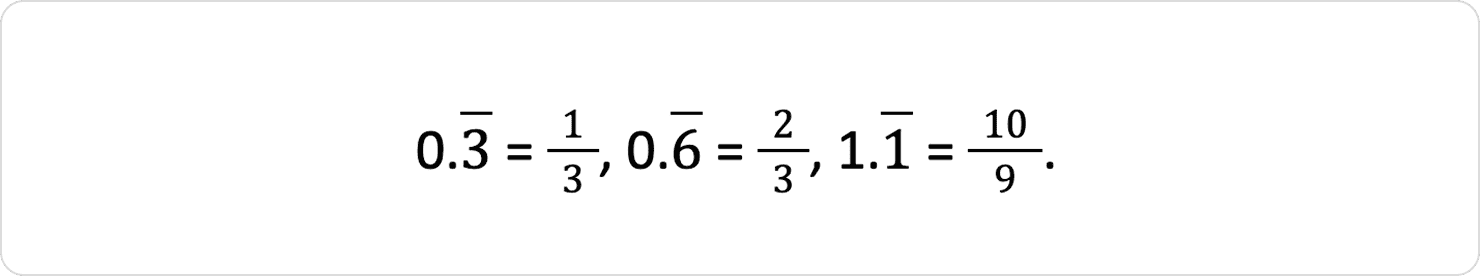
5. Нуль

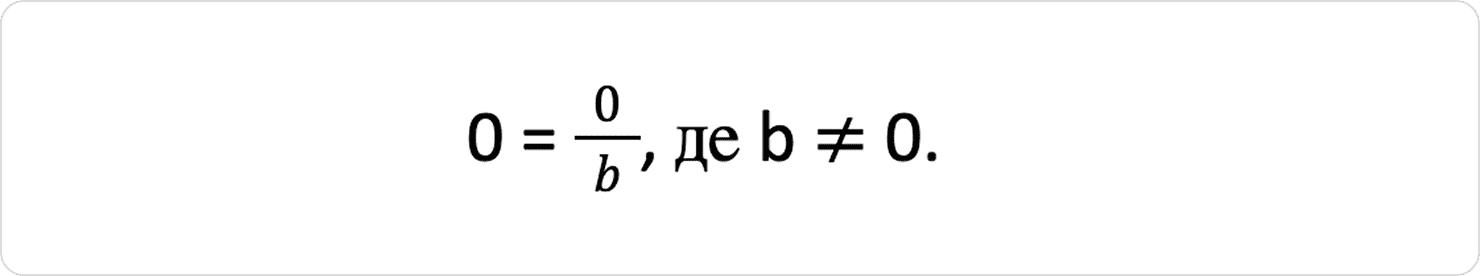
Отже, 0 — це також раціональне число.

Оскільки кожне з цих чисел можна подати у вигляді дробу — вони є раціональними.

У вигляді якого відношення можна подати кожне раціональне число?

Усі раціональні числа подаються у вигляді відношення двох цілих чисел:

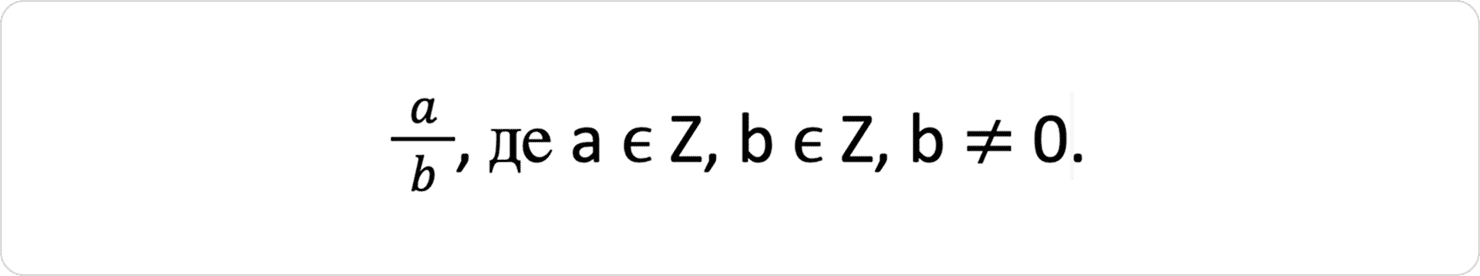
Це означає, що чисельник може бути додатним, від’ємним або нулем, а знаменник — будь-яким цілим числом, крім нуля.

Це ключова ознака раціональності: число, яке можна записати як дріб, — раціональне.

Важливо: не всі десяткові дроби є раціональними. Наприклад, число π або √2 — нераціональні, бо не мають точного дробового вираження.

Як множити раціональні числа?

Множення раціональних чисел — це одна з найпростіших дій із дробами.

Правило просте:

Щоб перемножити два дроби, потрібно перемножити чисельники між собою і знаменники між собою.

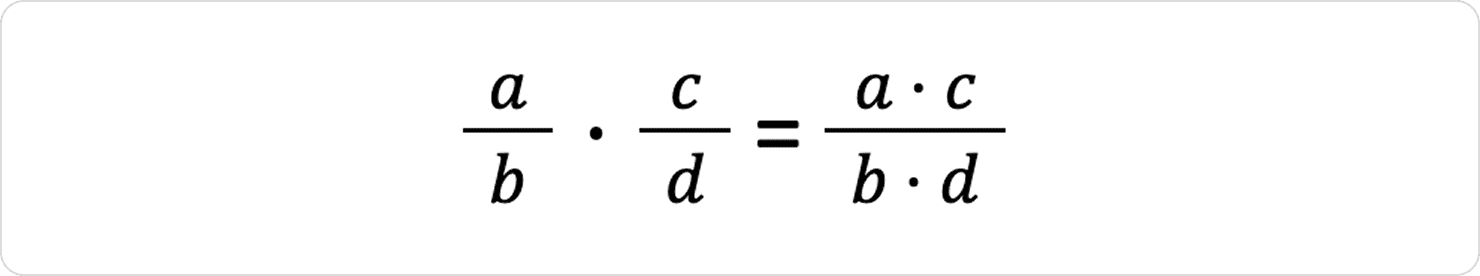
Це правило працює незалежно від того, чи маємо справу з додатними, від’ємними або нульовими значеннями.

Після множення не забудьте скоротити дріб, якщо це можливо.

Також важливо пам’ятати правила знаків:

• «плюс на плюс» — буде плюс,

• «мінус на мінус» — теж плюс,

• але «плюс на мінус» або «мінус на плюс» — вже мінус.

Нульова властивість множення: будь-яке число, помножене на 0, дорівнює 0.

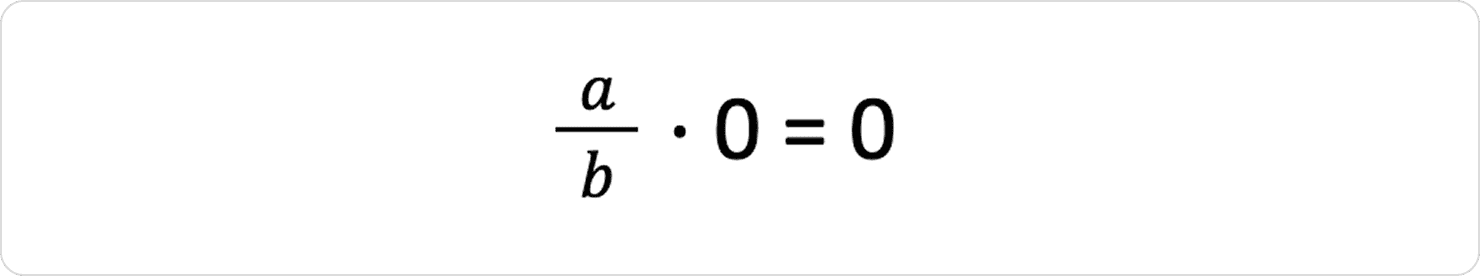
Множення раціональних чисел: приклади

Приклад 1:

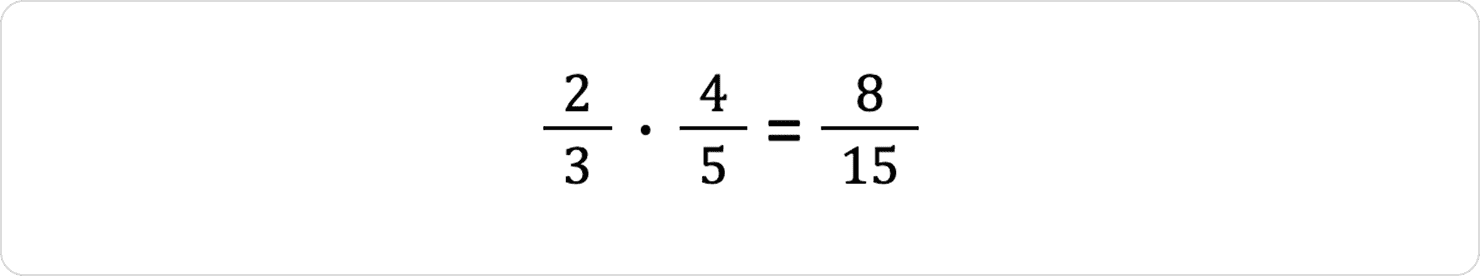
2 × 4 = 8

3 × 5 = 15

Приклад 2:

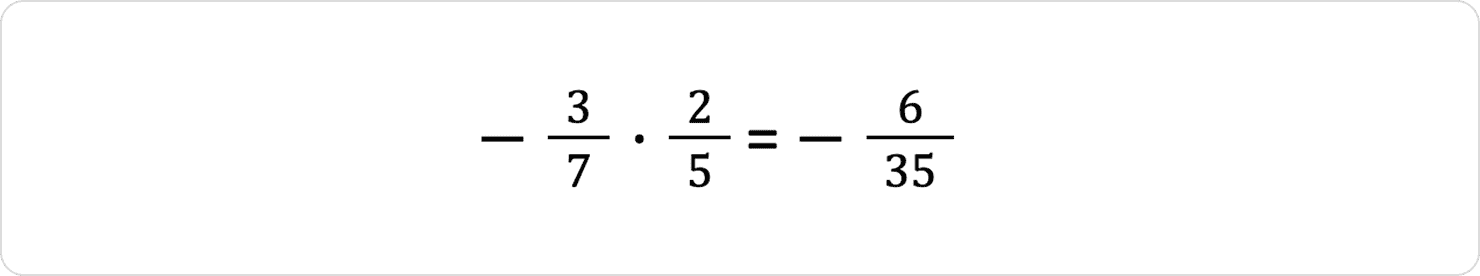
3 × 2 = 6

7 × 5 = 35

Не забуваємо про мінус у відповіді.

Приклад 3:

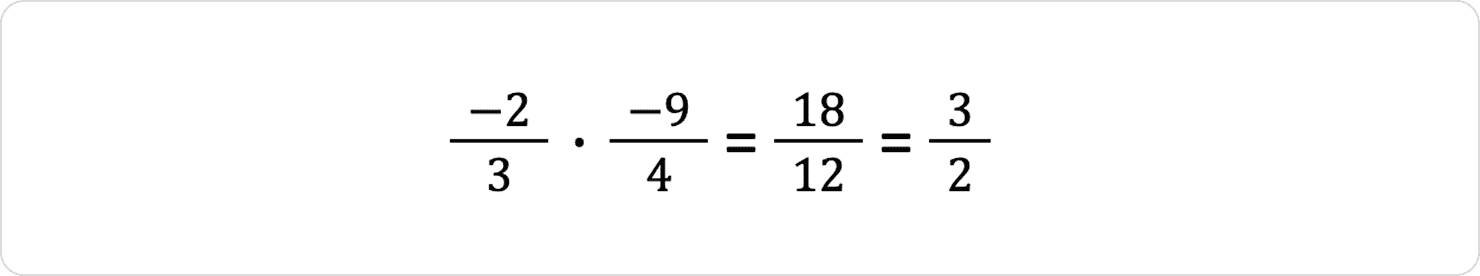
-2 × -9 = 18

3 × 4 = 12

Не забуваємо скоротити відповідь.

Приклад 4:

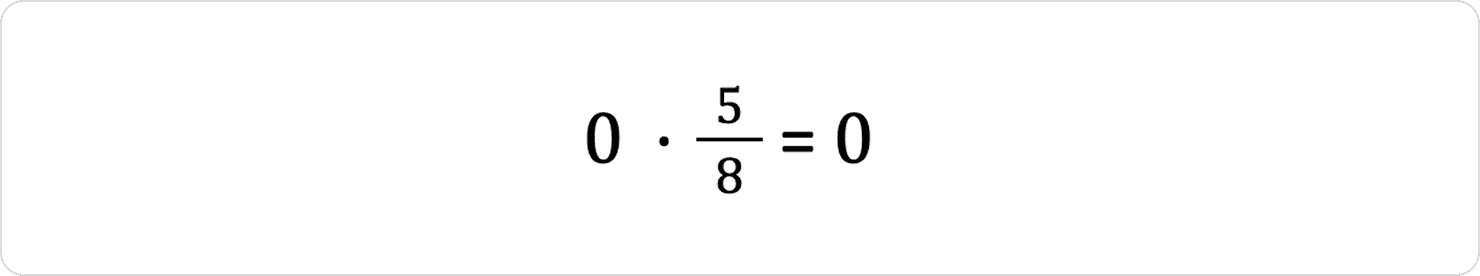
Нуль при множенні «обнуляє» все.

Навіщо потрібні раціональні числа?

Раціональні числа використовуються в повсякденному житті: у фінансових розрахунках, рецептах, подорожах, науці та навіть мистецтві (наприклад, в музиці — дроби для тривалості нот).

У шкільній математиці раціональні числа — це неодмінна частина програми, особливо у темах про дроби, відсотки, рівняння, функції. Їх потрібно вміти не лише впізнавати, а й використовувати в обчисленнях.

Вміння працювати з раціональними числами — ключ до успішної підготовки до НМТ з математики, адже ця тема зустрічається у багатьох завданнях. Вони часто фігурують у тестах у вигляді окремих завдань або частин більш складних задач. Тому важливо не просто «завчити», а зрозуміти суть теми.

Якщо ви хочете відчути впевненість у своїх знаннях і підготуватися до контрольних й іспитів без зайвого стресу — найкращим варіантом будуть індивідуальні заняття з досвідченим репетитором з математики.

Раціональні числа — це величезна категорія чисел, з якими ми постійно стикаємося у навчанні та житті. Вміння працювати з ними відкриває двері до розуміння складніших тем і успішного проходження тестувань.