Які формули з алгебри обов’язково потрібно знати? 8 клас

У 8 класі учні вчаться працювати з формулами, які допомагають швидше розв’язувати задачі, краще бачити структуру виразів і підходити до обчислень стратегічно. Багато з цих формул потрібні для підготовки до іспитів та НМТ. Тому, щоб полегшити процес навчання, ми зібрали для вас добірку найважливіших формул з алгебри за 8 клас — коротко, зрозуміло й з прикладами використання.

Які теми вивчаються в курсі алгебри 8 класу?

У 8 класі учні вивчають:

• Раціональні вирази.

Вчимося скорочувати дроби; зводити дроби до спільного знаменника; знаходити суму, різницю, добуток та частку дробів; виконувати тотожні перетворення раціональних виразів; розв’язувати рівняння зі змінною в знаменнику дробу; перетворювати степені з цілим показником; записувати числа в стандартному вигляді та будувати графіки функції у = k / х.

• Квадратні корені. Дійсні числа.

Вчимося застосовувати поняття арифметичного квадратного кореня для обчислення значень виразів; спрощувати вирази з коренями; розв’язувати рівняння, порівнювати значення виразів; перетворювати вирази із застосуванням винесення множника з-під знаку кореня чи внесення множника під знак кореня, звільнюватися від ірраціональності в знаменнику дробу; будувати графіки функцій y = x², y = √x та використовувати їх для досліджень.

• Квадратні рівняння.

Вчимося знаходити корені квадратних рівнянь; розкладати квадратний тричлен на множники; знаходити корені рівнянь, що зводяться до квадратних; складати і розв’язувати квадратні рівняння та рівняння, що зводяться до них, як математичні моделі прикладних задач.

• Сюжетні задачі.

Вчимося використовувати взаємозв’язки економічних явищ; знайомимося з видами податків та їх розрахунками, вчимося робити платежі; розраховувати продуктивність праці, вартість товару; рахувати сумісну роботу; працювати з сумішами та сплавами; розв’язувати задачі на рух.

Які формули за 8 клас потрібно знати на НМТ?

Розгляньмо найважливіші формули.

Степінь числа із цілим від’ємним показником:

Степінь з цілим від'ємним показником дорівнює дробу, чисельник якого дорівнює 1, а знаменник — степеню з тією ж основою і протилежним показником.

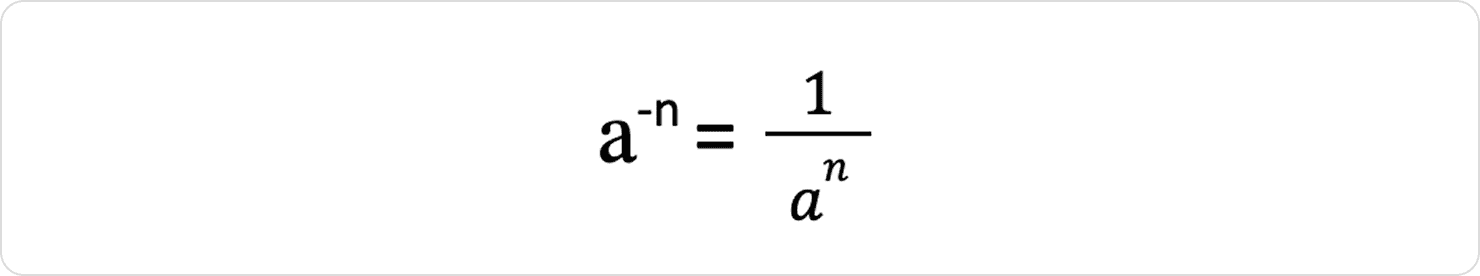
Степінь з показником, рівним нулю:

Будь-яке число, піднесене до нульового степеня, дорівнює одиниці. Це є загальним правилом для будь-якого числа, крім 0.

а⁰ = 1.

Стандартний вигляд числа:

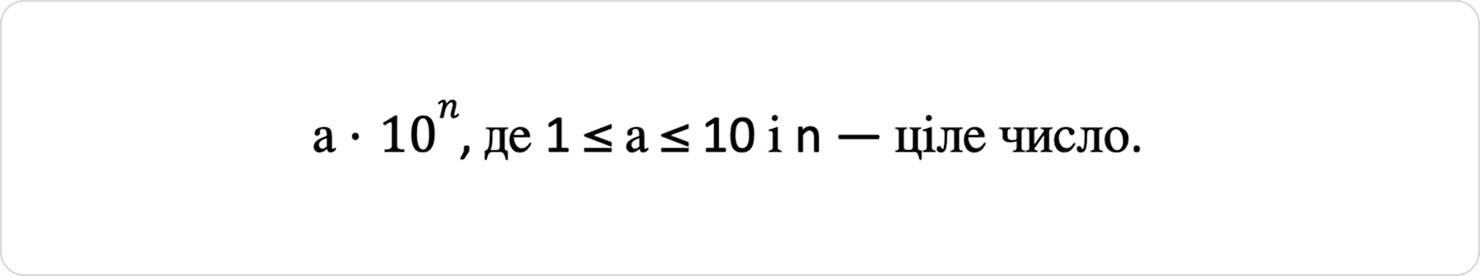
Властивості степеня із цілим показником:

а ≠ 0, b ≠ 0.

m, n — цілі.

Властивості функції:

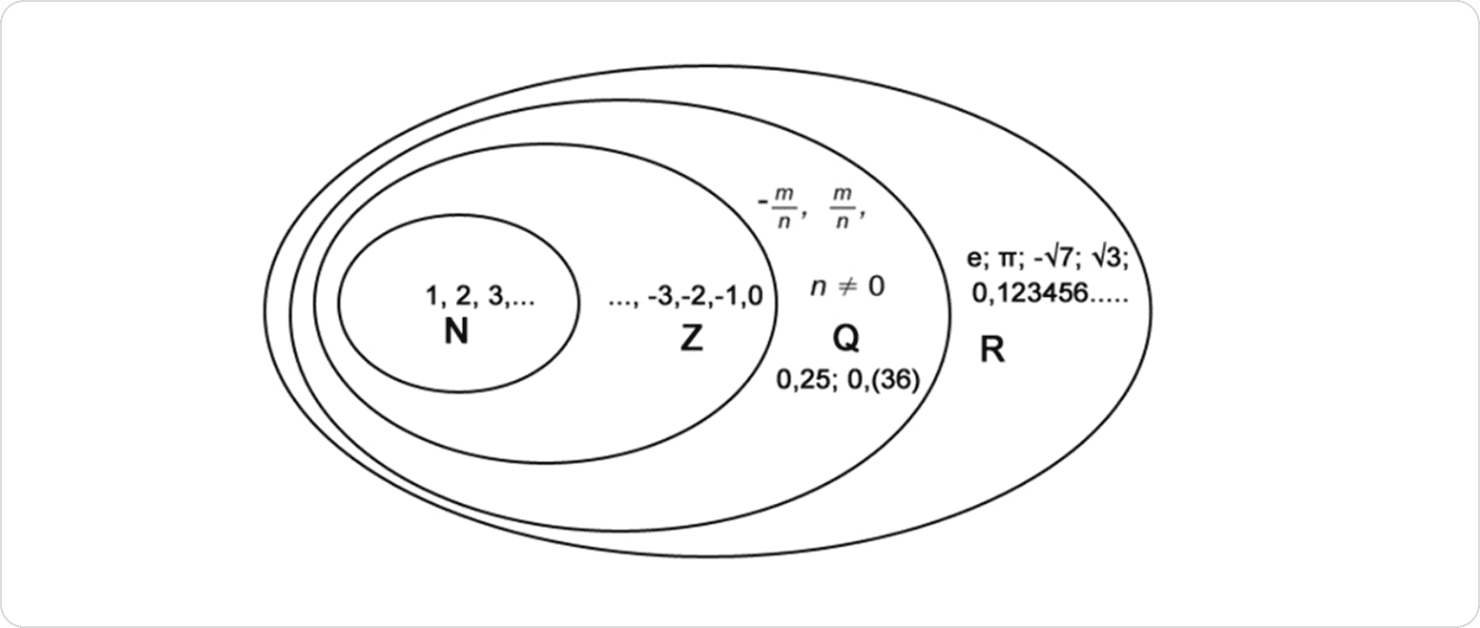
Числові множини:

Властивості арифметичного квадратного кореня:

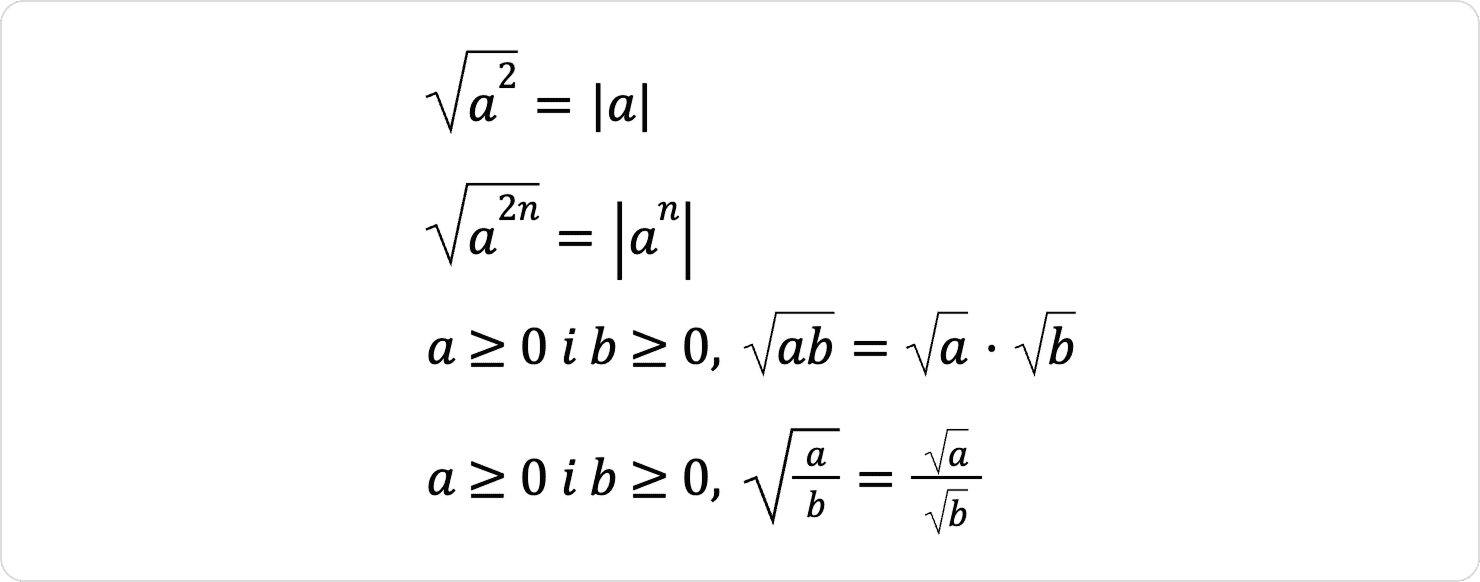
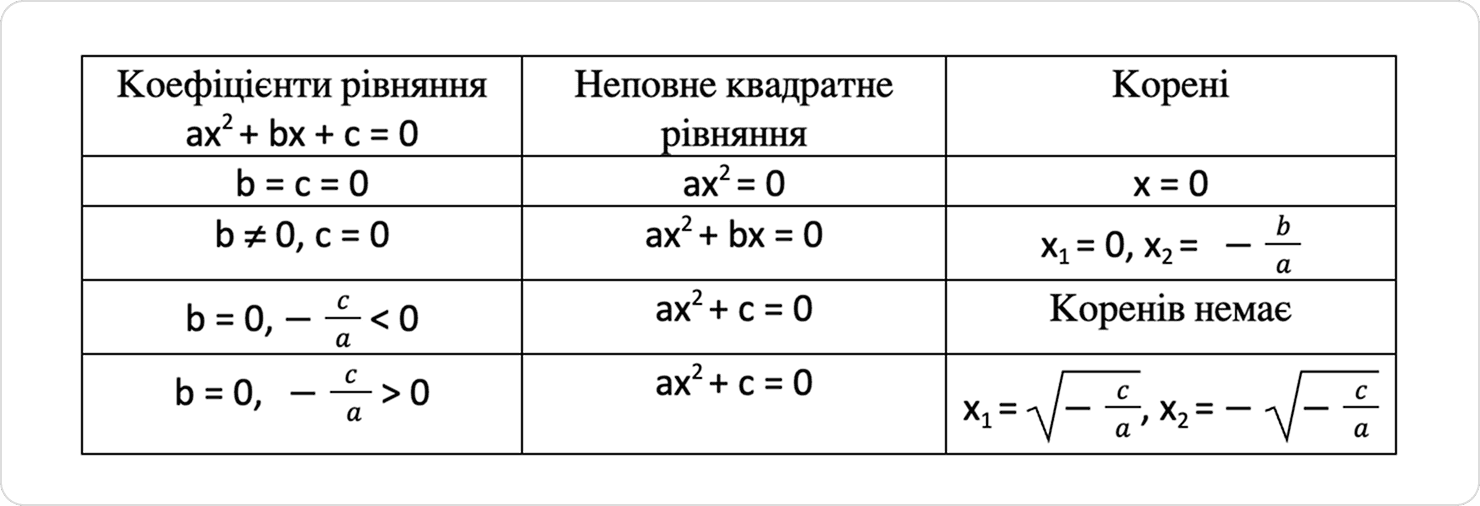
Розв’язування неповного квадратного рівняння:

Розв’язування квадратного рівняння ax² + bx + c = 0:

Теорема Вієта для зведеного квадратного рівняння x² + bx + c = 0:

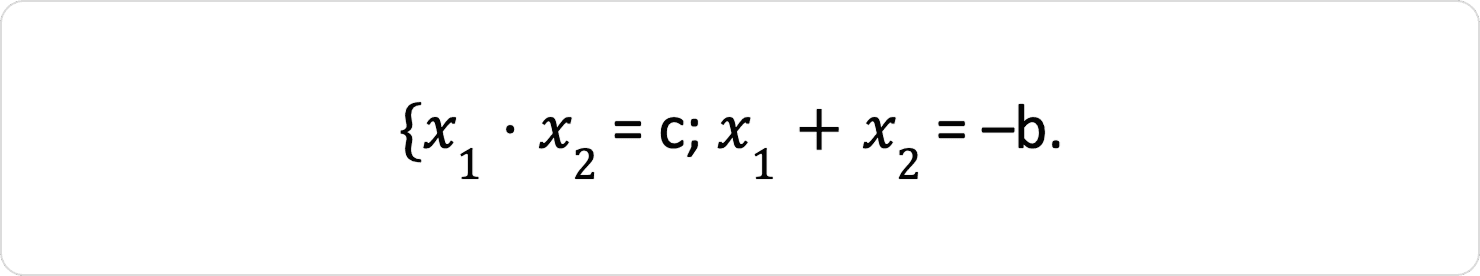
Розклад квадратного тричлена ax² + bx + c на множники, якщо D > 0:

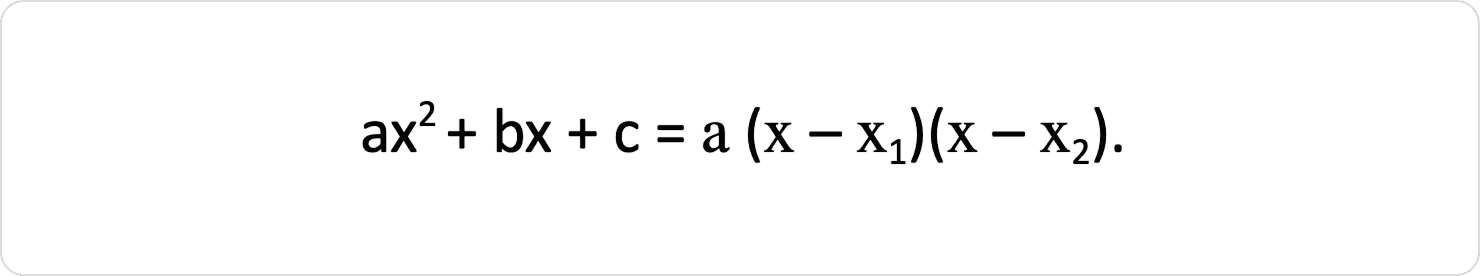
Розв’язування біквадратного рівняння x⁴ + bx² + c = 0 заміною:

x² = t, x⁴ = t².

Приклади застосування формул в завданнях НМТ

Приклад 1. 

Яке з наведених чисел є раціональним числом?

Відповідь: Д.

Приклад 2. 

Спростіть вираз:

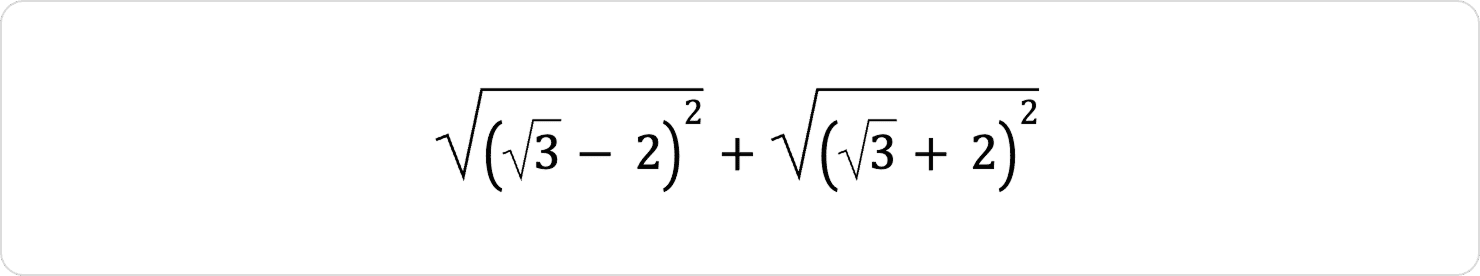
Розв’язок:

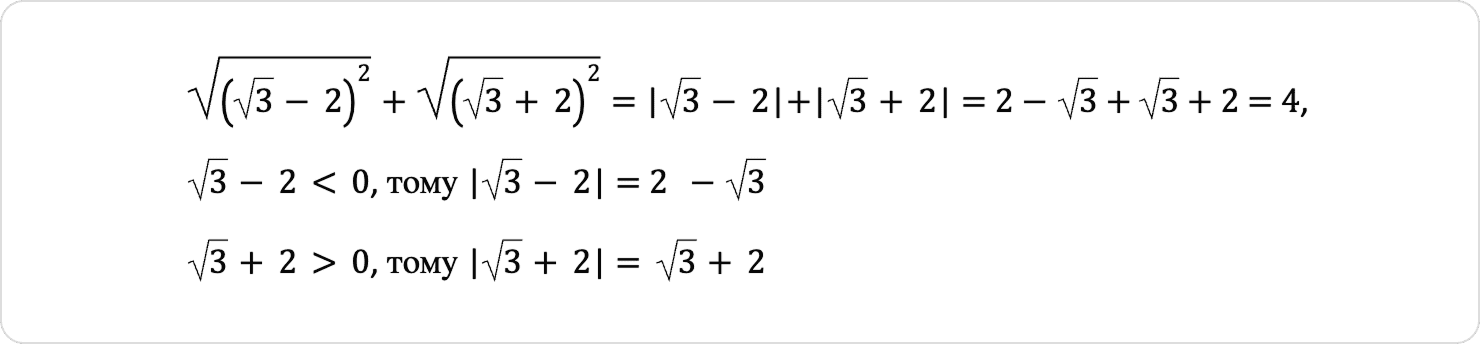
Відповідь: Г.

Приклад 3. 

Для кожного початку речення (1-3) доберіть його закінчення (А-Д) так, щоб утворилося правильне твердження, якщо а = –3.

Розв’язок:

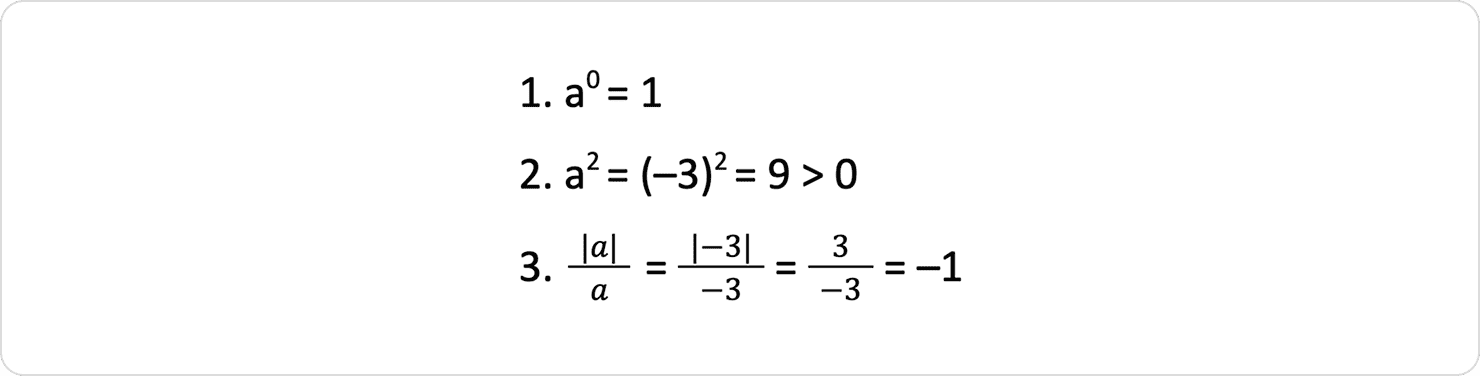
Відповідь: 1 — Б, 2 — А, 3 — Г.

Приклад 4. 

Спростіть вираз:

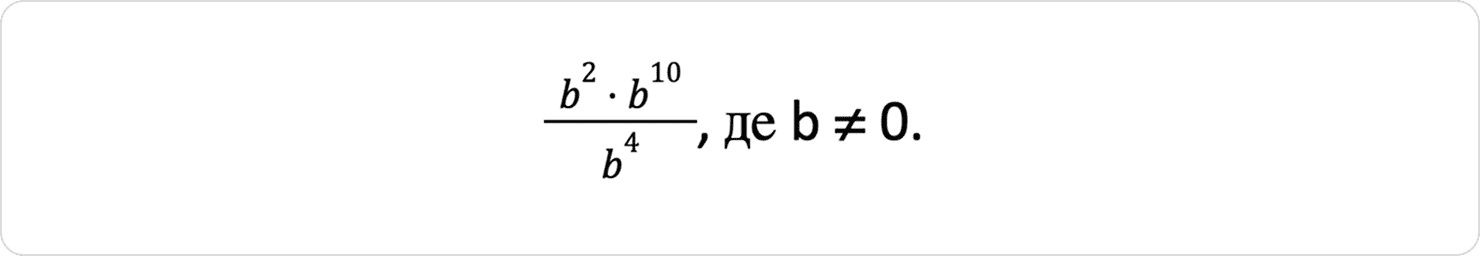
Розв’язок:

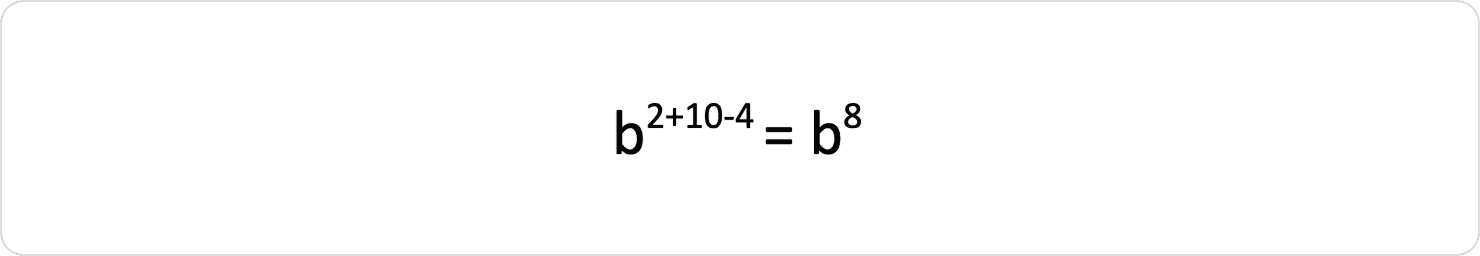
Відповідь: Б.

Приклад 5. 

Спростіть вираз:

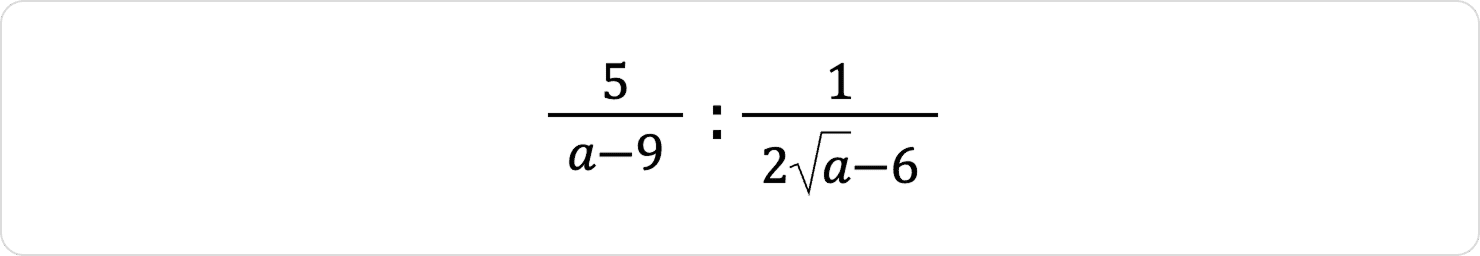
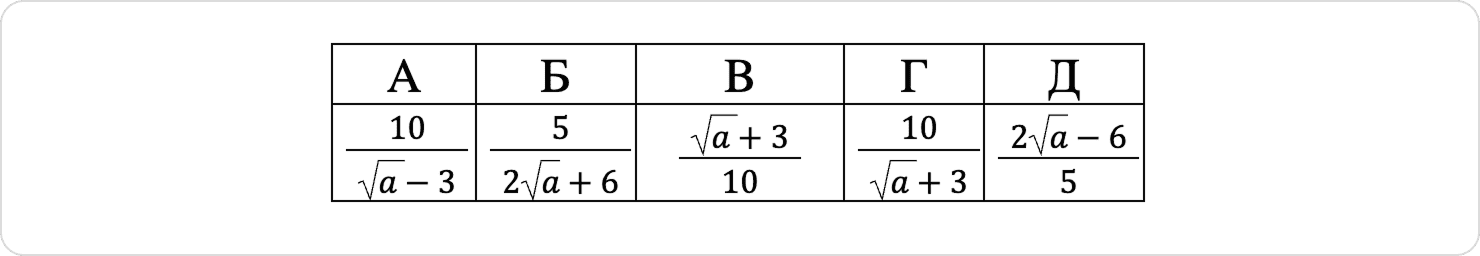
Розв’язок:

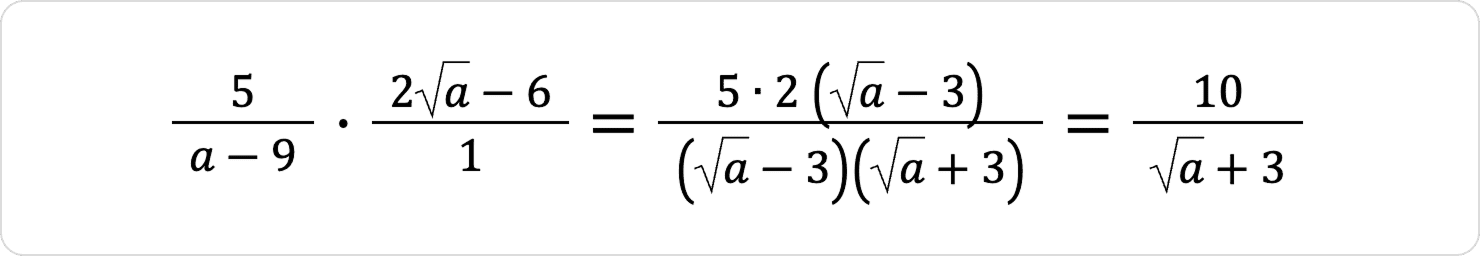
Відповідь: Г.

Приклад 6. 

Обчисліть добуток коренів рівняння x² + 6х – 55 = 0.

Варіанти відповідей:

А. –55

Б. 55

В. –6

Г. 6

Д. –49

Розв’язок:

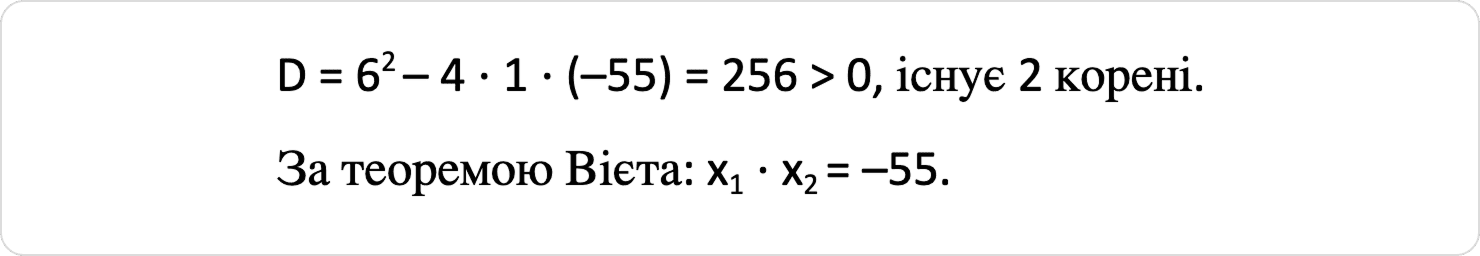
Відповідь: А.

Приклад 7. 

Розв’яжіть рівняння: x⁴ – x² – 20 = 0. У відповідь запишіть добуток усіх його дійсних коренів.

Розв’язок:

Відповідь: –5.

Приклад 8.

З пунктів А і В одночасно по шосе назустріч один одному виїхали два велосипедиста. Вони їхали без зупинок зі сталими швидкостями: перший — зі швидкістю x км/год, другий — зі швидкістю y км/год (х > у). Через t годин (t > 1) вони зустрілися у точці С і, не зупиняючись, продовжили рух без зміни напрямків. До кожного запитання (1-4) доберіть правильну відповідь (А-Д).

Запитання:

1. На скільки кілометрів зменшилася відстань по шосе між велосипедистами через 1 годину після початку руху?

2. Чому дорівнює відстань по шосе між пунктами А і В (у км)?

3. На скільки кілометрів більше проїхав перший велосипедист, ніж другий, за час від початку руху до моменту зустрічі?

4. За скільки годин перший велосипедист подолає відстань по шосе від точки С до пункту В?

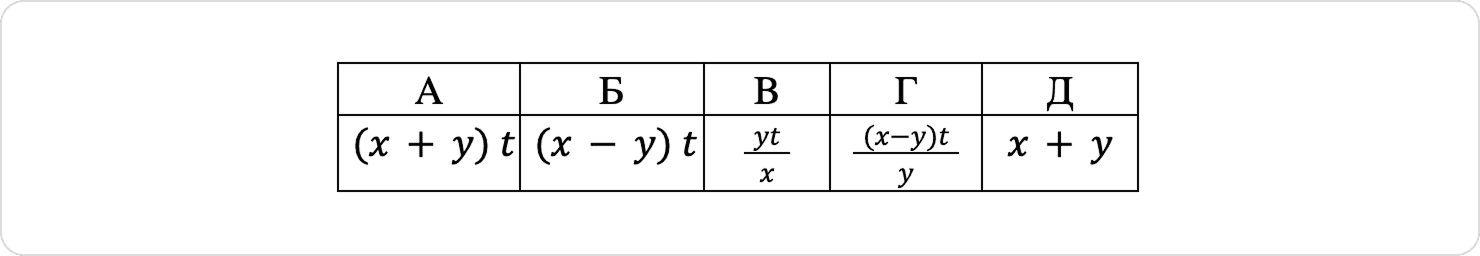
Розв’язок:

1. За 1 годину велосипедисти проїдуть (x + y) × 1 = x + y (км). На (x + y) зменшилася відстань по шосе між велосипедистами.

Відповідь: 1 — Д.

2. Через t годин велосипедисти зустрілися. Тому відстань між пунктами А і  В (x + y) t.

Відповідь: 2 — А.

3. За умовою х > у. За 1 годину перший велосипедист проїхав більше ніж другий на (x – y) км. За t годин різниця відстаней, які проїхали велосипедисти, становить (x – y) t.

Відповідь: 3 — Б.

4. Відстань СВ = yt км. Час, за який перший подолає відстань СВ, yt / x год.

Відповідь: 4 — В.

Сподіваємося, що цей конспект був для вас корисним!

А якщо вам потрібна детальніша допомога з програмою 8 класу або з підготовкою до НМТ — наші вчителі залюбки вам допоможуть!